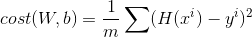Linear Regression
선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다. (출처 : 위키피디아)
선형 회귀 예시
- 아래 Table에 제시된 training data를 가지고 0~100의 선형적인 값을 갖는 y 값을 예측하는 Model을 만들자.
| x(hours) | y(score) |
|---|---|
| 10 | 96 |
| 9 | 89 |
| 2 | 47 |
| 3 | 64 |
| 5 | ? |
Hypothesis(가설)과 cost(loss, 손실)
-
위의 예시의 Data Set 을 늘려 아래와 같은 그래프로 나타내 보자.
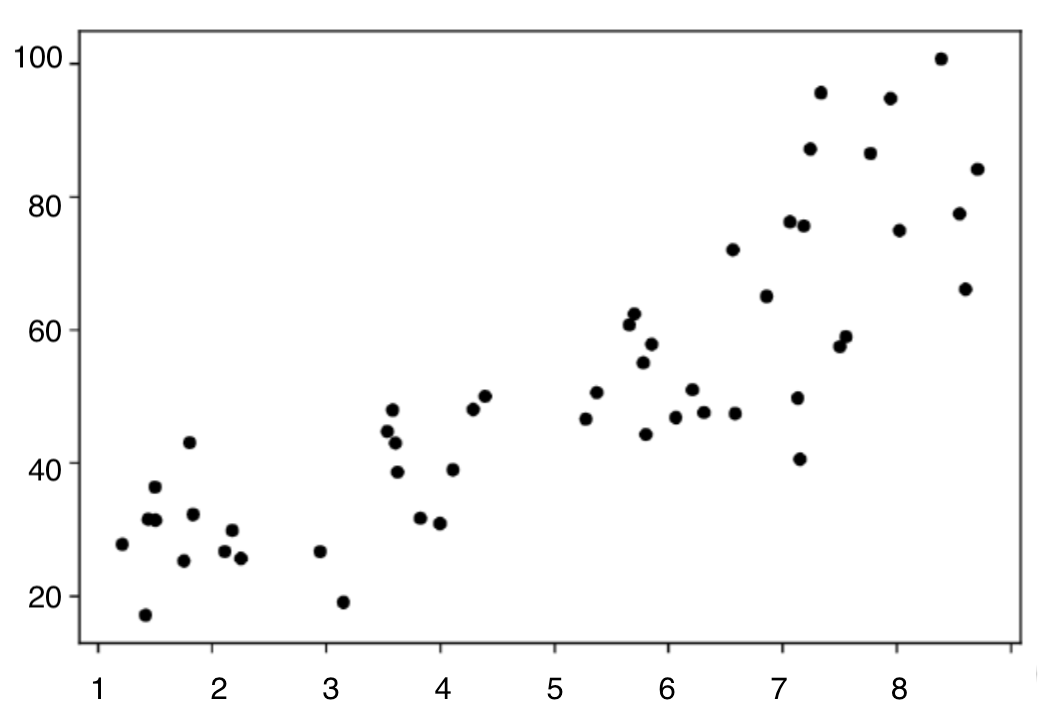
-
5시간 공부한 학생의 성적을 예측해 보려면 어떻게 해야할까?
- 기존 Data Set을 잘 나타낼 수 있는 그래프를 그린다.
- 여러 그래프 중 기존 Data Set에 가장 적합한 그래프를 찾는다.
- 2에서 찾은 그래프의 x값에 5를 넣어 그 때의 y값을 구한다.
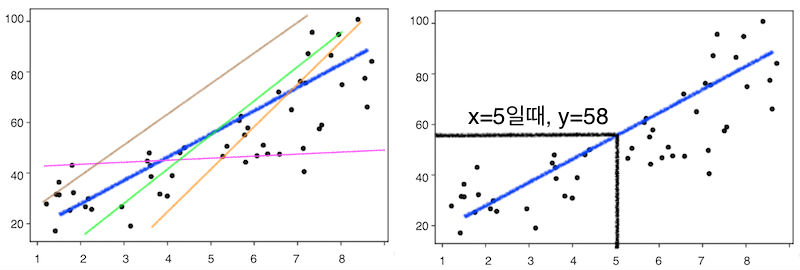
- 위의 과정을 살펴 보면,
1.가설(Hypothesis)을 설정하고,
2.손실(cost, loss)이 가장 작은 그래프를 찾는다.
Hypothesis(가설)
-
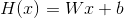
임의의 상수 W(weight)와 b(bias)를 갖는 x에 대한 1차 함수에서 x값에 대해 출력되는 H(x)를 얻을 수 있다.
Cost(loss, 손실)
우리의 목적은 W와 b에 임의의 값을 마구잡이로 넣어 가장 적합한 그래프를 찾는 것이다.
그러면 어떠한 그래프가 가장 적합한 그래프라고 할 수 있겠는가?
위 질문에 대한 해답이 cost이다.
우리의 가설에 의한 예측값(predict value)와 실제 값(true value)간의 차이가 발생하는데 이를 손실(cost 또는 loss)라고 한다.
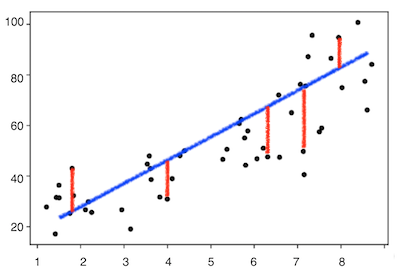
Cost Function
Cost Function은 위의 cost를 통해 가설과 실제 데이터가 얼마나 다른가?에 대한 값을 나타내준다.
Linear Regression Problem에서 Cost Function은 예측값과 실제값의 차이의 제곱 합에 의해 표현해준다.
우리는 이 Cost Function이 최소를 나타내는 가설(예측값과 실제값이 가장 적게 차이나는 가설)을 선정하여 최적의 Model을 구할 수 있다. cost가 작아지는 W, b를 찾아가는 과정을 학습이라고 할 수 있다.
Gradient Descent Algorithm
Gradient Descent Algorithm은 Cost Function이 최소값을 갖는 W와 b를 찾아가는 방법에 대한 알고리즘이다.
W와 b값을 반복적으로 값을 변경하며 최적의 W와 b값을 찾아 가야하는데, 무작정 임의의 값을 집어 넣는 것이 아니라
경사(Gradient)가 감소(descent)하는 방향으로 W와 b값을 조금씩(learning rate) 변경하여 cost를 계산하고, cost가 증가하지 않는 지점(local minimun)을 찾아 W와 b를 선정하는 방법이다.
- 다음 포스트에서는 예시를 통해 Linear Regression 문제에 대해 Model을 구하는 과정을 작성할 것이다.